Gewone en decimale breuken en acties daarover

Al in de basisschool worden studenten geconfronteerdfracties. En dan verschijnen ze in elk onderwerp. Je kunt de acties met deze nummers niet vergeten. Daarom moet u alle informatie over gewone en decimale breuken kennen. Deze concepten zijn eenvoudig, het belangrijkste is om alles in de juiste volgorde te begrijpen.

Waarom heb je breuken nodig?

De wereld om ons heen bestaat uit hele objecten. Daarom is er in nooddelen geen sprake van. Maar het dagelijks leven duwt mensen voortdurend om met delen van dingen en dingen te werken.

Chocolade bestaat bijvoorbeeld uit verschillende lobben. Overweeg de situatie wanneer de tegel wordt gevormd door twaalf rechthoeken. Als het in tweeën is verdeeld, dan blijken het 6 delen te zijn. Ze zal goed verdeeld zijn in drie. Maar de vijf zullen niet in staat zijn om een ​​heel aantal chocoladestukjes te geven.

Overigens zijn deze segmenten al breuken. En hun verdere verdeling leidt tot het verschijnen van meer complexe getallen.

Wat is een "breuk"?

Dit nummer bestaat uit delen van de eenheid. Extern ziet het eruit als twee nummers gescheiden door een horizontale of schuine streep. Deze functie wordt fractioneel genoemd. Het nummer dat bovenaan is geschreven (links) wordt de teller genoemd. Wat van onderaf staat (aan de rechterkant) is de noemer.

In feite is een fractionele lijn een teken van verdeling. Dat wil zeggen, de teller kan deelbaar worden genoemd en de noemer kan een deler worden genoemd.

Wat zijn de breuken?

In de wiskunde zijn er slechts twee soorten: gewone en decimale breuken. Met de eerste studenten maken ze kennis met de basislessen en noemen ze gewoon 'breuken'. De tweede leer in groep 5. Het is dan dat deze namen verschijnen.

Gewone breuken zijn al die fracties die zijn geschrevende vorm van twee nummers gescheiden door een lijn. Bijvoorbeeld 4/7. Decimaal is het getal waarin het fractionele deel een positierecord heeft en door een komma van het geheel is gescheiden. Bijvoorbeeld 4.7. Studenten moeten duidelijk begrijpen dat de twee gegeven voorbeelden totaal verschillende aantallen zijn.

Elke eenvoudige breuk kan worden geschreven als een decimaal. Deze uitspraak is bijna altijd waar in de tegenovergestelde richting. Er zijn regels waarmee je een decimale breuk kunt schrijven met een gewone breuk.

Welke ondersoorten hebben dit soort breuken?

Start beter in chronologische volgorde, zoals ze worden bestudeerd. De eerste zijn gewone breuken. Onder hen zijn er 5 ondersoorten.

1. Correct. De teller is altijd minder dan de noemer.

2. Wrong. De teller is groter dan of gelijk aan de noemer.

3. Reduceerbaar / onherleidbaar. Het kan correct of incorrect zijn. Een ander belangrijk ding is of de teller met de noemer gemeenschappelijke factoren heeft. Als dat het geval is, moeten beide delen van de breuk worden gedeeld, dat wil zeggen, verminderen.

4. Mixed. Aan zijn gebruikelijke correcte (onjuiste) fractionele deel, wordt een geheel getal toegewezen. En het staat altijd aan de linkerkant.

5. Component. Het is gevormd uit twee verdeelde fracties. Dat wil zeggen, het heeft drie fractionele kenmerken tegelijk.

Decimale breuken hebben slechts twee ondersoorten:

• laatste, dat wil zeggen, een waarvan het fractionele deel is begrensd (heeft een einde);

• oneindig - een getal waarvan de cijfers na de komma niet eindigen (ze kunnen eindeloos worden geschreven).

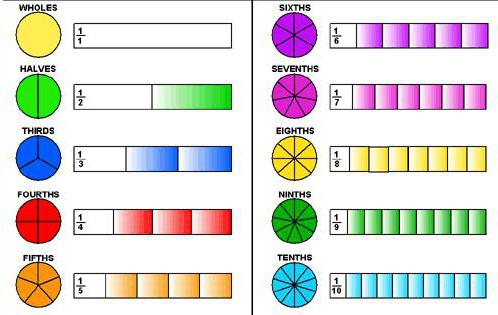
Hoe een decimaal in een gewone breuk omzetten?

Als dit een eindig getal is, wordt een associatie op basis van de regel toegepast - zoals ik hoor, dus ik schrijf. Dat wil zeggen, je moet het correct lezen en opschrijven, maar zonder een komma, maar met een gebroken lijn.

Als een aanwijzing over de noodzakelijke noemer, moet je onthouden dat het altijd een en meerdere nullen zijn. Deze laatste moeten zoveel als de cijfers in het fractionele deel van het aantal dat wordt beschouwd, schrijven.

Hoe decimalen in gewone breuken te converteren,als hun hele aandeel afwezig is, dat wil zeggen, is gelijk aan nul? Bijvoorbeeld 0,9 of 0,05. Na het toepassen van deze regel, is het gebleken dat u nul gehele getallen moet schrijven. Maar het is niet gespecificeerd. Het blijft om alleen fractionele delen op te schrijven. Voor de eerste is de noemer 10 en de tweede 100. Dat wil zeggen dat de aangegeven voorbeelden nummers 9/10, 5/100 hebben. En de laatste blijkt met 5 te zijn ingekort. Daarom moet het resultaat hiervan 1/20 zijn.

Hoe maak je een decimale breuk,als het gehele deel ervan verschilt van nul? Bijvoorbeeld 5.23 of 13.00108. In beide voorbeelden wordt het hele deel gelezen en de waarde ervan geschreven. In het eerste geval is dit 5, in het tweede geval 13. Dan moeten we naar het fractionele gedeelte gaan. Ze zouden dezelfde bewerking met hen moeten uitvoeren. Het eerste nummer verschijnt 23/100, het tweede - 108/100000. De tweede waarde moet opnieuw worden verlaagd. In het antwoord worden deze gemengde fracties verkregen: 5 23/100 en 13 27/25000.

Hoe een oneindig decimaal in een gewone decimale breuk omzetten?

Als het niet-periodiek is, is een dergelijke bewerking niet mogelijk. Dit feit houdt verband met het feit dat elke decimale breuk altijd wordt vertaald naar de finale of naar de periodieke.

Het enige dat hiermee mag worden gedaanbreuken, is eromheen. Maar dan zal het decimaal ongeveer gelijk zijn aan dat oneindige. Het kan al worden omgezet in een gewoon exemplaar. Maar het omgekeerde proces: vertalen naar decimalen geeft nooit een beginwaarde. Dat wil zeggen dat oneindige niet-periodieke fracties in gewone fracties niet worden vertaald. Je moet dit onthouden.

Hoe schrijf je een oneindige periodieke breuk in de vorm van een gewoon?

In deze cijfers, na de komma,een of meer cijfers die worden herhaald. Ze worden een menstruatie genoemd. Bijvoorbeeld 0,3 (3). Hier "3" in de periode. Ze zijn geclassificeerd als rationeel, omdat ze kunnen worden omgezet in gewone breuken.

Degenen die periodieke fracties tegenkwamen,het is bekend dat ze puur of gemengd kunnen zijn. In het eerste geval begint de punt direct vanaf de komma. In de tweede - het fractionele deel begint met willekeurige getallen, en dan begint de herhaling.

De regel waarmee u in het formulier wilt schrijvengewone fractie van oneindig decimaal, zal verschillend zijn voor de twee aangegeven typen getallen. Pure periodieke breuken om gewoon te schrijven zijn vrij eenvoudig. Net als bij het eindige moeten ze worden getransformeerd: noteer in de teller de punt en de noemer het getal 9, zo vaak herhaald als het getal de punt bevat.

Bijvoorbeeld 0, (5). Het hele deel van het nummer is dat niet, dus je moet onmiddellijk fractioneel beginnen. In de teller schrijf 5, en in de noemer van één 9. Dat wil zeggen, het antwoord is een fractie van 5/9.

De regel over het noteren van een gewone decimale periodieke breuk, die gemengd is.

• Tel de cijfers van het fractionele deel vóór de periode. Ze geven het aantal nullen in de noemer aan.

• Kijk naar de lengte van de periode. Zoveel zal een noemer hebben.

• Noteer de noemer: eerste negen, dan nul.

• Om de teller te bepalen, moet u het verschil van twee cijfers noteren. De verlagingen zijn alle cijfers achter de komma, samen met de punt. Aftrekbaar - het is hetzelfde zonder een menstruatie.

Bijvoorbeeld 0.5 (8) - noteer de periodiekedecimale breuk in de vorm van gewoon. In het fractionele deel is er tot de periode één cijfer. Dus nul zal er een zijn. Ook in de periode is slechts één cijfer 8, dat wil zeggen één is er negen. Dat wil zeggen dat het in de noemer nodig is om 90 te schrijven.

Om de teller van 58 te bepalen, moet je 5 aftrekken. Het blijkt 53 te zijn. Het antwoord op het voorbeeld zou zijn om 53/90 te schrijven.

Hoe worden gewone breuken omgezet naar decimalen?

De eenvoudigste versie is een getal waarvan de noemer 10, 100, enzovoort is. Dan wordt de noemer eenvoudigweg weggegooid en wordt er een komma geplaatst tussen de fractionele en de hele delen.

Er zijn situaties waarin de noemer eenvoudig isverandert in 10, 100, enz. Bijvoorbeeld de nummers 5, 20, 25. Ze worden vermenigvuldigd met respectievelijk 2, 5 en 4. Alleen vermenigvuldigen wordt niet alleen de noemer toegewezen, maar ook de teller met hetzelfde nummer.

Voor alle andere gevallen is een eenvoudige regel handig: deel de teller door de noemer. In dit geval kunt u twee varianten van antwoorden krijgen: het laatste of het periodieke decimaalteken.

Acties met gewone breuken

Optellen en aftrekken

Met hen maken studenten kennis met anderen. En eerst hebben de breuken dezelfde noemers, en dan verschillend. Algemene regels kunnen worden teruggebracht tot een dergelijk plan.

1. Zoek het kleinste gemene veelvoud van de noemers.

2. Schrijf aanvullende factoren op alle gewone breuken.

3. Vermenigvuldig de tellers en noemers met de factoren die voor hen zijn opgegeven.

4. Tel de getallen van breuken (aftrekken) op en laat de gemeenschappelijke noemer ongewijzigd.

5. Als de teller van het gereduceerde getal kleiner is dan het subtraged, moeten we nagaan of we een gemengd getal of een juiste breuk hebben.

6. In het eerste geval moet het hele stuk de eenheid bezetten. Voeg een noemer toe aan de teller van de breuk. En voer vervolgens de aftrekking uit.

7. In de tweede - het is noodzakelijk om de regel van aftrekken toe te passen vanaf een kleiner aantal groter. Dat wil zeggen, trek de module van de subtrahend-module af en plaats het "-" -teken als antwoord.

8. Kijk zorgvuldig naar het resultaat van optellen (aftrekken). Als een onregelmatige breuk wordt verkregen, moet het hele stuk worden toegewezen. Dat wil zeggen, om de teller te delen door de noemer.

Vermenigvuldigen en delen

Om ze uit te voeren hoeven fracties niet tot een gemeenschappelijke noemer te leiden. Dit vereenvoudigt de uitvoering van acties. Maar ze moeten nog steeds de regels volgen.

1. Bij het vermenigvuldigen van gewone breuken, is het noodzakelijk om getallen in tellers en noemers te beschouwen. Als een teller en een noemer een gemeenschappelijke vermenigvuldiger hebben, kunnen deze worden verminderd.

2. Vermenigvuldig de tellers.

3. Vermenigvuldig de noemers.

4. Als het een reduceerbare breuk blijkt te zijn, moet het opnieuw vereenvoudigd worden.

5. Bij delen moeten we eerst de deling door vermenigvuldiging en de deler (de tweede breuk) vervangen door de omgekeerde breuk (de teller en noemer omwisselen).

6. Handel vervolgens als vermenigvuldiging (beginnend met punt 1).

7. In taken waarbij u een geheel getal moet vermenigvuldigen (delen), moet dit laatste worden geschreven in de vorm van een onjuist getal. Dat is, met de noemer 1. Handel dan zoals hierboven beschreven.

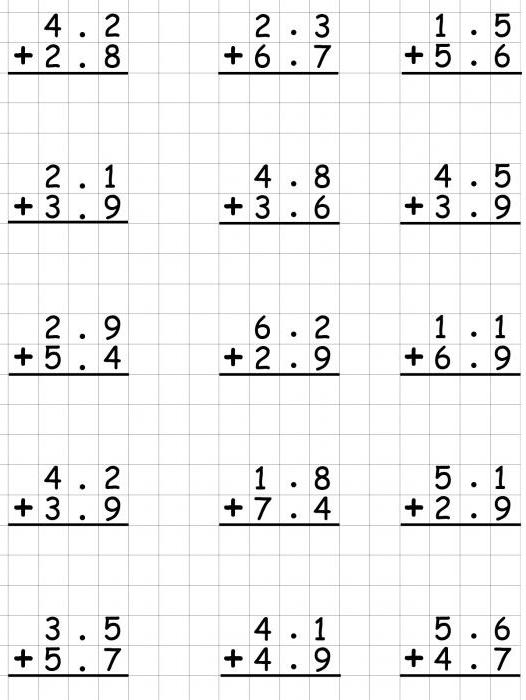
Acties met decimalen

Optellen en aftrekken

U kunt natuurlijk altijd een decimaal draaienin het gewone. En handel volgens het reeds beschreven plan. Maar soms is het handiger om zonder deze vertaling te handelen. Dan zullen de regels voor het optellen en aftrekken exact hetzelfde zijn.

1. Gelijk aan het aantal cijfers in het fractionele deel van het getal, dat wil zeggen na de komma. Wijs het ontbrekende aantal nullen toe.

2. Schrijf de breuk zodat de komma onder de komma staat.

3. Toevoegen (aftrekken) als natuurlijke getallen.

4. Neem de komma af.

Vermenigvuldigen en delen

Het is belangrijk dat u hier geen nullen hoeft toe te voegen. Breuken zouden moeten blijven zoals ze in het voorbeeld zijn weergegeven. En ga dan verder volgens plan.

1. Om te vermenigvuldigen, moet je fracties onder elkaar schrijven, geen aandacht schenken aan komma's.

2. Vermenigvuldigen, als natuurlijke getallen.

3. Zet een komma in het antwoord, geteld vanaf het rechter einde van het antwoord, zoveel getallen als ze zijn in de fractionele delen van beide vermenigvuldigers.

4. Om te delen, moet je eerst de deler omzetten: maak er een natuurlijk getal van. Dat wil zeggen, vermenigvuldig het met 10, 100, enz., Afhankelijk van het aantal cijfers in het deel van de deler.

5. Om het dividend met hetzelfde aantal te vermenigvuldigen.

6. Deel het decimaal in een natuurlijk getal.

7. Zet een komma in het antwoord op het moment dat het hele stuk klaar is.

Wat als er in één voorbeeld beide soorten breuken zijn?

Ja, in de wiskunde zijn er vaak voorbeelden, indie acties op gewone en decimale breuken moeten uitvoeren. In dergelijke taken zijn er twee mogelijke oplossingen. Het is noodzakelijk om de aantallen objectief te wegen en de optimale te kiezen.

De eerste manier: gewoon decimaal introduceren

Het is geschikt als, bij delen of vertaleneindige fracties worden verkregen. Als ten minste één nummer een periodiek deel geeft, is deze methode verboden. Daarom, zelfs als je niet van gewone breuken houdt, moet je ze tellen.

De tweede manier: decimalen noteren door gewoon

Deze methode is gedeeltelijk handigna het decimaalteken zijn er 1-2 cijfers. Als er meer zijn, kunt u een zeer grote gewone breuk krijgen en met decimale notaties kunt u de taak sneller en eenvoudiger tellen. Daarom moet u de taak altijd nuchter evalueren en de eenvoudigste oplossingsmethode kiezen.